Question

Most US adults have social ties with a large number of people, including friends, family, co-workers, and other acquaintances. It is nearly impossible for most people to reliably list all the people they know, but using a mathematical model, social analysts estimate that, on average, a US adult has social ties with 634 people.1 A survey of 1700 randomly selected US adults who are cell phone users finds that the average number of social ties for the cell phone users in the sample was 664 with a standard deviation of 778. Does the sample provide evidence that the average number of social ties for a cell phone user is significantly different from 634, the hypothesized number for all US adults?

Answer 1

The statistical hypothesis test comparing the average of 664 social ties from a sample to the hypothesized 634 average suggests examining the z-score and p-value to determine if there is a significant difference.

Step-by-step explanation:

To determine if the average number of social ties for a cell phone user is significantly different from 634, the hypothesized average for all US adults, we conduct a hypothesis test. With a sample average of 664 social ties and a standard deviation of 778 from a sample size of 1700 adults, we can use statistical methods to test for significance.

The null hypothesis (H0) is that the true mean number of social ties for cell phone users is 634 (the same as for all US adults). The alternative hypothesis (H1) is that the true mean is not equal to 634. We would calculate the z-score from the sample mean using the formula:

• Z = (Sample mean - Hypothesized mean) / (Standard deviation / sqrt(Sample size))

Given that the calculated z-score is compared against the critical z-value at a certain significance level (e.g., 0.05), we determine if there is enough evidence to reject the null hypothesis. If the p-value is lower than the significance level, the result is statistically significant, implying a difference in the average number of social ties.

Answer 2

No, the sample does not provide evidence that the average number of social ties for a cell phone user is significantly different from 634.

Step-by-step explanation:

In this case we need to determine whether the average number of social ties for a cell phone user is significantly different from 634 people.

The hypothesis can be defined as follows:

H₀: The average number of social ties for a cell phone user is 634 people, i.e. μ = 634.

Hₐ: The average number of social ties for a cell phone user is different from 634 people, i.e. μ ≠ 634.

The information provided is:

`n=1700\\\bar x=664\\SD=778`

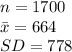
As the sample size is quite large, i.e. n = 1700 > 30 and is taken form an unknown population, according to the Central limit theorem the sampling distribution of sample mean will follow the Normal distribution.

So, a z-test for single mean will be applied to perform the test.

Compute the test statistic value as follows:

`z=(\bar x-\mu)/(SD/√(n))\\\\=(664-634)/(778/√(1700))\\\\=1.59`

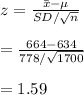
The test statistic value is 1.59.

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected.

Compute the p-value for the two-tailed test as follows:

`p-value=2\cdot P(Z >1.59)\\=2* [1-P(Z<1.59)]\\=2* (1-0.944)\\=0.112`

*Use a z-table for the probability.

The p-value of the test is 0.112.

The p-value of the test is very large for all the commonly used significance level. The null hypothesis will not be rejected.

Thus, there is not enough evidence to conclude that the average number of social ties for a cell phone user is different from 634 people.