Answer:
AQ = 20 units
Explanation:
Comparing triangle AQR to ABC,
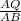 =
=
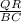
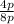 =
=
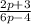
cross multiply and make p the subject of formula, we have:
8p (2p+3) = 4p(6p-4)
16
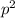 + 24p = 24
+ 24p = 24
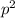 - 16p
- 16p
24p + 16p = 24
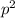 - 16
- 16
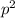
40p = 8
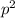
divide through by 8p,
p = 5
Therefore, AQ = 4p
= 4 × 5
= 20
AQ = 20 units