Question

PLEASE HELP!! 30 POINTS

The stray-cat population in a small town grows exponentially. In 1999 the town had 35 stray cats, and the relative growth rate was 18% per year.

(a) Find the function that models the stray-cat population n(t) after t years.



(b) Find the projected population after 6 years.



(c) Find the number of years required for the stray-cat population to reach 700.

Answer 1

a)
`N(t) = 35e^(0.18t)`

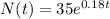
b) The projected population after 6 years is of 103 stray cats.

c) The number of years required for the stray-cat population to reach 700 is 16.64.

Explanation:

The population N(t) after t years, following an exponential growth moel, is given by:

`N(t) = N(0)e^(rt)`

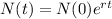
In which N(0) is the initial population and r is the growth rate.

In 1999 the town had 35 stray cats, and the relative growth rate was 18% per year.

This means that
`N(0) = 35, r = 0.18`

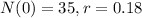
(a) Find the function that models the stray-cat population n(t) after t years.

`N(t) = N(0)e^(rt)`

`N(t) = 35e^(0.18t)`

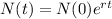
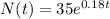
(b) Find the projected population after 6 years.

This is N(6).

`N(t) = 35e^(0.18t)`

`N(6) = 35e^(0.18*6)`

`N(6) = 103`

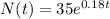
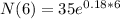
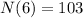
The projected population after 6 years is of 103 stray cats.

(c) Find the number of years required for the stray-cat population to reach 700.

This is t for which N(t) = 700. So

`N(t) = 35e^(0.18t)`

`700 = 35e^(0.18t)`

`e^(0.18t) = (700)/(35)`

`e^(0.18t) = 20`

`\ln{e^(0.18t)} = ln(20)`

`0.18t = ln(20)`

`t = (ln(20))/(0.18)`

`t = 16.64`

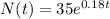
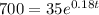
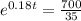
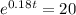
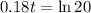
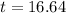
The number of years required for the stray-cat population to reach 700 is 16.64.