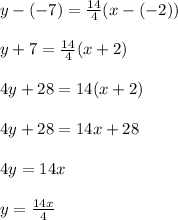Question

Find an equation for the perpendicular bisector of the line segment whose endpoints are (5,-9)and (-9,-5)

Answer 1

y = ¹⁴/₄.x

Explanation:

First of, if the bisector is perpendicular to the line segment, then we can find the gradient of the bisector (
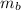`m_(b)`) using the rule/principle:

Let:

m = gradient of the line segment

Then:

`m_(b)` =
`-(1)/(m)`

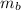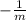
We can find m since we have two points that fall on the line segment, (5, -9) and (-9, -5):

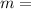`m =` Δy/Δx

`m = (-9 - (-5))/(5 - (-9)) \\\\ m = -(4)/(14)`

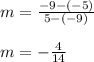
We can now find
`m_(b)`:

`m_(b) = -(1)/((-(4)/(14)) ) \\\\ m_(b) = 1.(14)/(4) \\\\ m_(b) = (14)/(4)`

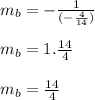
The equation of a line can be found using:

y - y₁ = m(x - x₁)

We have the gradient of the perpendicular bisector, the only other thing we need to identify the equation of the bisector is coordinates of a point that fall on the line;

We know the line will pass through the point exactly midway between (5, -9) and (-9, -5) since it is a bisector;

This can be found by:

`x_(1) = -9 + (5 - (-9))/(2) \\ x_(1) = -9 + 7 \\ x_(1) = -2 \\\\ y_(1) = -5 + (-9 - (-5))/(2) \\ y_(1) = -5 +(-2) \\ y_(1) = -7 \\\\ (-2, -7)`

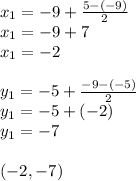
We have a point on the line and the gradient so we can now find the equation:

`y - (-7) = (14)/(4)(x - (-2)) \\\\ y + 7 = (14)/(4)(x + 2) \\\\ 4y + 28 = 14(x + 2) \\\\ 4y + 28 = 14x + 28 \\\\ 4y = 14x \\\\ y = (14x)/(4)`