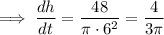Question

PLEASE HELP THIS IS AP CALCULUS IM LOSING MY MIND

A cup has the shape of a right circular cone. The height of the cup is 16 cm, and the radius of the
cm opening is 4 cm. Water is being poured into the cup at a constant rate of 3 cm. At what rate, in
cm per second, is the water level rising when the depth of the water in the cup is 6 cm? (The volume of a cone of height h and radius r is given by V=1/3pir^2h.

1. 1/64pi
2. 3/pi
3. 4/3pi
4. 9/4pi

Answer 1

3.
`(4)/(3 \pi)`

Explanation:

Volume of a cone:

`V=\frac13\pi r^2h`

(where r is the radius and h is the height)

Given:

• h = 16 cm
• r = 4 cm

`\implies r=\frac14h`

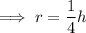
Therefore, substitute
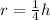`r=\frac14h` into the volume formula to find the volume of the cone in terms of h:

`\implies V=\frac13\pi \left(\frac14h\right)^2h`

`\implies V=(1)/(48)\pi h^3`

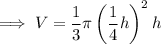
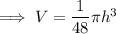
Differentiate with respect to h:

`\implies (dV)/(dh)=3 \cdot (1)/(48) \pi h^2=(\pi h^2)/(16)`

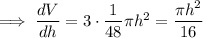
Volume is increasing at a constant rate of 3cm/s:

`\implies (dV)/(dt)=3`

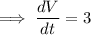
Use the chain rule to find
`(dh)/(dt)`

`\implies (dh)/(dt)=(dV)/(dt)*(dh)/(dV)`

`\implies (dh)/(dt)=3*(16)/(\pi h^2)`

`\implies (dh)/(dt)=(48)/(\pi h^2)`

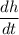
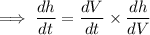
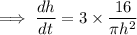
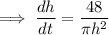
When h = 6:

`\implies (dh)/(dt)=(48)/(\pi \cdot 6^2)=(4)/(3 \pi)`