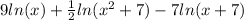Explanation:
Begin by separating the division. Division in the argument of a logarithm function is equivalent to subtracting the log of the numerator and denominator:
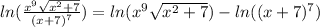
Multiplication under a logarithm means addition:
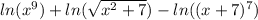
Log rules say that exponents can be dragged to the front as coefficients: