Answer:
The mean oil-change time that would there be a 10% chance of being at or below is 15.46 minutes.
Explanation:
We are given that records indicate that the mean time is 16.2 minutes, and the standard deviation is 3.4 minutes.
On a typical Saturday, the oil-change facility will perform 35 oil changes between 10 A.M. and 12 P.M. Assuming that data follows normal distribution.
Let
 = sample mean time
= sample mean time
The z score probability distribution for sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean time = 16.2 minutes
= population mean time = 16.2 minutes
 = standard deviation = 3.4 minutes
= standard deviation = 3.4 minutes
n = sample size = 35 oil changes
Now, the mean oil-change time that would there be a 10% chance of being at or below is given by;
P(X
 x) = 0.10 {where x is required mean oil-change time}
x) = 0.10 {where x is required mean oil-change time}
P(


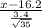 ) = 0.10
) = 0.10
P(Z

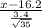 ) = 0.10
) = 0.10
Now, in the z table the critical value of X which represents the below 10% of the probability area is given as -1.282, that means;
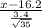 = -1.282
= -1.282
x - 16.2 =

x = 16.2 - 0.74 = 15.46 minutes
Hence, the mean oil-change time that would there be a 10% chance of being at or below is 15.46 minutes.