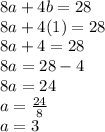Question

Solve the following system of equations for a and for b:

Value of a
value of b
System of Equations:
9a + 3b = 30
8a + 4b = 28

Answer 1

`a=3\\b=1`

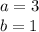
Explanation:

`9a+3b=30\\8a+4b=28`

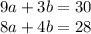
Let's solve the second equation for a to later on replace it in the first equation.

`8a+4b=28\\8a=28-4b\\a=(28-4b)/(8)`

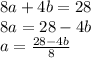
Now plug this into the first equation.

`9a+3b=30\\9((28-4b)/(8))+3b=30`

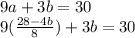
Distribute the 9

`((252-36b)/(8)) +3b=30`

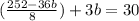
Break down the fraction.

`(252)/(8)-(36b)/(8)+3b=30`

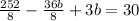
Simplify.

`(63)/(2)-(9)/(2)b+3b=30`

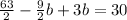
Subtract
`(63)/(2)`

`-(9)/(2)b+3b=30-(63)/(2)`

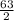
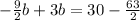
Combine like terms.

`(-9+2*3)/(2)b=(30*2-63)/(2)`

`(-9+6)/(2)b=(60-63)/(2)`

`(-3)/(2)b=(-3)/(2)`

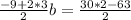
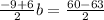
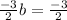
Muliply by the reciprocal or inverted fraction next to b.

`(-(2)/(3))(-(3)/(2)) b=-(3)/(2)(-(2)/(3))`

`b=1`

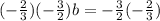
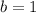
Now plug this value into any of the equations to find the value of a.

`8a+4b=28\\8a+4(1)=28\\8a+4=28\\8a=28-4\\8a=24\\a=(24)/(8)\\ a=3`