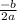Question

Will give 25 points for a good explanation/answer

Answer 1

A real solution (in agreement with statement d in your list of answer options)

Explanation:

Recall that the expression
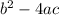`b^2-4ac` is what is called the "discriminant" of a quadratic equation of the form:
`a\,x^2+b\,x+c=0`

and such is because, the possible solutions for the unknown x" of such equation are given by the quadratic formula:

`x=(-b+-√(b^2-4ac) )/(2a)`

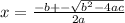
and if you notice, inside the square-root symbol you find exactly the expression
`b^2-4ac`

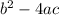
This is called the discriminant because it allows us to discriminate, discern how many and the type of solutions the equation can have.

Notice that if this discriminant is zero, the expression inside the square root becomes zero, and square root of zero is zero. That means that the quadratic formula will render not two, but a solution which is real:

The real number that derives from making the quotient of the real numbers:

`(-b)/(2a)`