The question is not typed properly! The correct and complete question is given below.
Question:
Suppose that among the population of smartphone owners with 16 GB of storage, the mean amount of storage used is 13 GB and the standard deviation is 3 GB. A consumer research group regularly takes random samples of 50 of these customers and calculates the mean amount of storage Calculate the mean and standard deviation of the sampling distribution x bar.
You may round to one decimal place.
Given Information:
Population mean smartphone storage = μ = 13 GB
Population Standard deviation = σ = 3 GB
Sample size = n = 50
Required Information:
Mean of the sampling distribution = ?
Standard deviation of the sampling distribution = ?
Answer:
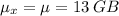
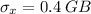
Step-by-step explanation:
We are given that the mean storage among smartphones owners is 13 GB with a standard deviation of 3 GB.
A random sample of 50 smartphone owners is selected from the population.
We want to find out the the mean and standard deviation of this sampling distribution.
Recall from the central limit theorem, if the sample size is large enough (n ≥ 30) then the sampling distribution approaches normal distribution.
A normal distribution is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean.
Since the sample size is large enough ( n = 50) in this case then the mean of the sampling distribution is given by
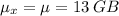
The mean of the sampling distribution will be same as population mean.
The standard deviation of the sampling distribution is given by
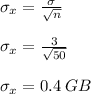
Therefore, the standard deviation of the sampling distribution is 0.4 GB.