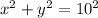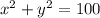Question

Give the equation of the circle centered at the origin and passing through the point(0,10)

Answer 1

`x^(2) + y^(2) = 100`

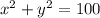
Explanation:

The equation of a circle has the following format:

`(x - x_(0))^(2) + (y - y_(0))^(2) = r^(2)`

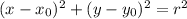
In which r is the radius(half the diameter) and the centre is the point
`(x_(0), y_(0))`

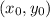
Centered at the origin

This means that
`x_(0) = 0, y_(0) = 0`

Passing through the point(0,10)

The radius is the distance of any point in which the circle passes to the centre.

Using the formula for the distance between two points.

`r = D = \sqrt{(0 - 0)^(2) + (10 - 0)^(2)} = 10`

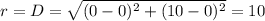
So

`x^(2) + y^(2) = 10^(2)`

`x^(2) + y^(2) = 100`