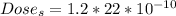Question

Potassium is a crucial element for the healthy operation of the human

body. Potassium occurs naturally in our environment (and thus our
bodies) as three isotopes: Potassium-39, Potassium-40, and Potassium-
41. Their current abundances are 93.26%, 0.012% and 6.728%. A typical
human body contains about 3.0 grams of Potassium per kilogram of body
mass.
1. How much Potassium-40 is present in a person with a mass of 80
kg?
2 If, on average, the decay of Potassium-40 results in 1.10 MeV of
energy absorbed, determine the effective dose (in Sieverts) per year
due to Potassium-40 in an 80-kg body. Assume an RBE of 1.2. The
half-life of Potassium-40 is 1.28 x 10° years.
​

Answer 1

1

The mass of the Potassium-40 is
`m_(40)} = 2.88*10^(-6) kg`

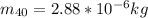
2

The Dose per year in Sieverts is
`Dose_s = 26.4 *10^(-10)`

Step-by-step explanation:

From the question we are told that

The isotopes of potassium in the body are Potassium-39, Potassium-40, and Potassium- 41

Their abundance is 93.26%, 0.012% and 6.728%

The mass of potassium contained in human body is
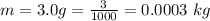`m = 3.0 g = (3)/(1000) = 0.0003 \ kg` per kg of the body

The mass of the first body is
`m_1 = 80 \ kg`

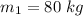
Now the mass of potassium in this body is mathematically evaluated as

`m_p = m * m_1`

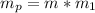
substituting value

`m_p = 80 * 0.0003`

`m_p =0.024 kg`

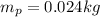
The amount of Potassium-40 present is mathematically evaluated as

`m_(40)} =`0.012% * 0.024

`m_(40)} = (0.012)/(100) * 0.024`

`m_(40)} = 2.88*10^(-6) kg`

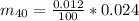
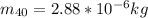
The dose of energy absorbed per year is mathematically represented as

`Dose = (E)/(m_1)`

Where E is the energy absorbed which is given as
`E = 1.10 MeV = 1.10 * 10^6 * 1.602*10^(-19)`

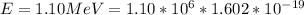
Substituting value

`Dose = ( 1.10 * 10^6 * 1.602*10^(-19))/(80)`

`Dose = 22*10^(-10) J/kg`

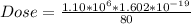
The Dose in Sieverts is evaluated as

`Dose_s = REB * Dose`

`Dose_s = 1.2 * 22*10^(-10)`

`Dose_s = 26.4 *10^(-10)`