Answer:
Explanation:
Analysis of the Data Given:
For sample 1 , the sample size

number of favorable cases
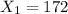
thus ; the sample proportion is
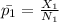
=
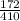
= 0.4195
For sample 2, the sample size

number of favorable cases
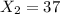
Then the sample proportion is
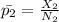
=
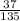
= 0.2741
The value of the pooled proportion is computed as
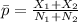
=
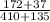
= 0.3835
We are also given that the significance level is
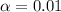
Null Hypothesis :
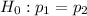 : the proportion of workers that say monitoring employee e-mail is unethical is not greater than the proportion of bosses.
: the proportion of workers that say monitoring employee e-mail is unethical is not greater than the proportion of bosses.
Alternative hypothesis :
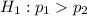 : the proportion of workers that say monitoring employee e-mail is unethical is greater than the proportion of bosses.
: the proportion of workers that say monitoring employee e-mail is unethical is greater than the proportion of bosses.
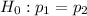 :
:
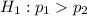 :
:
The above corresponds to the right-tailed test , for which a z-test for the two population proportions needs to be conducted .
Rejection Region:
From the given information ; the significance level is
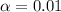
Then; the critical value for a right tailed test is
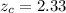
The rejection region for this right tailed test is R = {z : z > 2.33}
Test Statistics:
The z-statistic is computed as:

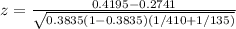
z = 3.014
Decision about the null hypothesis:
Since it is observed that z = 3.014 >
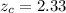 ; it is concluded that the null hypothesis is rejected
; it is concluded that the null hypothesis is rejected
Using the P-value approach: The P-value p = 0.0013 and since p = 0.0013<0.01 , it is concluded that the null hypothesis is rejected.
Conclusion:
It is concluded that the proportion of workers that say monitoring employee e-mail is unethical is greater than the proportion of bosses.