Question

A gambler has a coin which is either fair (equal probability heads or tails) or is biased with a probability of heads equal to 0.3. Without knowing which coin he is using, you ask him to flip the coin 10 times. If the number of heads is at least 4, you conclude that the coin is fair. If the number of heads is less than 4, you conclude that the coin is biased.

(a) What is the probability you reach an incorrect conclusion if the coin is fair?

(b) What is the probability that you reach an incorrect conclusion if the coin is biased?

Answer 1

(a) 0.1719

(b) 0.3504

Explanation:

For every coin the number of heads follows a Binomial distribution and the probability that x of the 10 times are heads is equal to:

`P(x)=(n!)/(x!(n-x)!)*p^x*(1-p)^(10-x)`

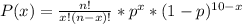
Where n is 10 and p is the probability to get head. it means that p is equal to 0.5 for the fair coin and 0.3 for the biased coin

So, for the fair coin, the probability that the number of heads is less than 4 is:

`P(x<4 )=P(0)+P(1)+P(2)+P(3)`

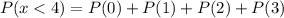
Where, for example, P(0) and P(1) are calculated as:

`P(0)=(10!)/(0!(10-0)!)*0.5^0*(1-0.5)^(10-0)=0.0009\\P(1)=(10!)/(1!(10-1)!)*0.5^1*(1-0.5)^(10-1)=0.0098`

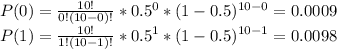
Then,
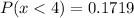`P(x<4 )=0.1719`, so there is a probability of 0.1719 that you conclude that the coin is biased given that the coin is fair.

At the same way, for the biased coin, the probability that the number of heads is at least 4 is:

`P(x\geq4 )=P(4)+P(5)+P(6)+...+P(10)`

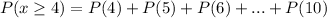
Where, for example, P(4) is calculated as:

`P(4)=(10!)/(4!(10-4)!)*0.3^4*(1-0.3)^(10-4)=0.2001`

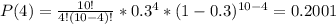
Then,
`P(x\geq4 )=0.3504`, so there is a probability of 0.3504 that you conclude that the coin is fair given that the coin is biased.