Question

A paint manufacturer has a uniform annual demand for 16,000 cans of automobile primer. It costs $4 to store one can of paint for one year and $500 to set up the plan for the production of the primer. Let x be the number of cans of paint produced during each production run, and let y be the number of production runs.

Then the setup cost is 500y and the storage cost is 2x, so the total storage and setup cost is C = 500y +2x. Furthermore, xy = 16,000 to account for the annual demand.
How many times a year should the company produce this primer in order to minimize the total storage and setup costs?

A. The company should have 6 production runs each year.
B. The company should have 8 production runs each year.
C. The company should have 10 production runs each year.
D. The company should have 11 production runs each year

Answer 1

B) The company should have 8 production runs each year

Step-by-step explanation:

Given :

Uniform annual demand, = 16000

Total cost, C = 500y + 2x

xy = 16000

`x = (16000)/(y)`

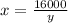
Let's substitute
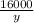`(16000)/(y)` for x in C.

Therefore, we have :

`C = 500y + 2( (16000)/(y) )`

`C = 500y + (32000)/(y)`

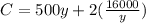
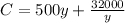
In order to minimize the total storage and setup costs,

Differentiating wrt y:

`C = C_m_i_n, (dc)/(dy)=0`

`C'(y) = 500y + (32000)/(y^2) = 0`

`y^2 = (320)/(5) = 64`

`y = √(64) = 8`

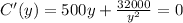
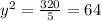
In order to minimize the total storage and setup costs, the company should have 8 production runs each year