Question

If Tanisha has ​$1000 to invest at 7​% per annum compounded semiannually​, how long will it be before she has ​$1600​? If the compounding is​ continuous, how long will it​ be?

Answer 1

Using continuous interest 6.83 years before she has ​$1600​.

Using continuous compounding, 6.71 years.

Explanation:

Compound interest:

The compound interest formula is given by:

`A(t) = P(1 + (r)/(n))^(nt)`

Where A(t) is the amount of money after t years, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per unit year and t is the time in years for which the money is invested or borrowed.

Continuous compounding:

The amount of money earned after t years in continuous interest is given by:

`P(t) = P(0)e^(rt)`

In which P(0) is the initial investment and r is the interest rate, as a decimal.

If Tanisha has ​$1000 to invest at 7​% per annum compounded semiannually​, how long will it be before she has ​$1600​?

We have to find t for which
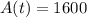`A(t) = 1600` when
`P = 1000, r = 0.07, n = 2`

`A(t) = P(1 + (r)/(n))^(nt)`

`1600 = 1000(1 + (0.07)/(2))^(2t)`

`(1.035)^(2t) = (1600)/(1000)`

`(1.035)^(2t) = 1.6`

`\log{1.035)^(2t)} = \log{1.6}`

`2t\log{1.035} = \log{1.6}`

`t = \frac{\log{1.6}}{2\log{1.035}}`

`t = 6.83`

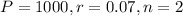
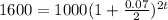
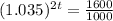
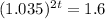
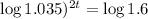
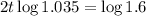
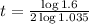
Using continuous interest 6.83 years before she has ​$1600​

If the compounding is​ continuous, how long will it​ be?

We have that
`P(0) = 1000, r = 0.07`

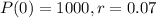
Then

`P(t) = P(0)e^(rt)`

`1600 = 1000e^(0.07t)`

`e^(0.07t) = 1.6`

`\ln{e^(0.07t)} = ln(1.6)`

`0.07t = ln(1.6)`

`t = (ln(1.6))/(0.07)`

`t = 6.71`

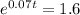
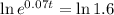
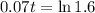
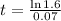
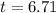
Using continuous compounding, 6.71 years.