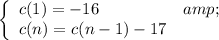Question

Complete the recursive formula of the arithmetic sequence, -16,-33,-50,-67,...

c(1)=
c(n)=c(n-1)+

Answer 1

The recursive formula of the arithmetic sequence is

`\left\{ \begin{array}{ll} c(1)=-16 & \\ c(n)=c(n-1)-17 \end{array} \right.`

Explanation:

A recursive formula designates the starting term,
`a_1`, and the nth term of the sequence,
`a_n`, as an expression containing the previous term (the term before it),
`a_(n-1)`.

Recursive formulas give us two pieces of information:

1. The first term of the sequence
2. The pattern rule to get any term from the term that comes before it

From the arithmetic sequence
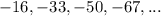`-16,-33,-50,-67,...`, the first term is -16 and the rule to get any term from its previous term is add -17.

Therefore, the recursive formula should look as follows:

`\left\{ \begin{array}{ll} c(1)=-16 & \\ c(n)=c(n-1)-17 \end{array} \right.`