Question

What is the value of n in the equation 32 × 33 = 3n?

Answer 1

Answer: The value of
`n` is 5

Explanation:

-Solve:

`3^2` ×
`3^3`
`=3^n`

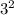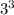
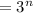
-If two numbers with exponents are multiplying together, then the exponents would add up together:

`3^5 = 3^n`

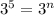
-Simplify by the exponent:

`243 = 3^n`

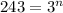
-Take the logarithm both sides of the equation:

`log(3^n)= log (243)`

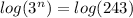
- Then, you divide both sides by
`log (3)` :

`n=(log(243))/(log(3))`

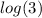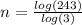
- Use the change-of-base formula, which is
`(log(a))/(log(b)) = log_(b)(a)`:

`n = log_(3)(243)`

`n = 5`

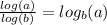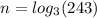
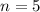
So, the value of
`n` is 5.

Answer 2

5

Explanation:

u can add 2 and 3 when their base number (3) are the same