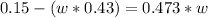Answer:
The angular velocity of the wheel is

Step-by-step explanation:
From the question we are told that
The mass of the toy train is

The speed of the train is
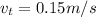
The radius of the wheel is
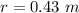
The mass of the wheel is
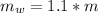
According to the law of conservation of momentum

Where
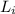 is the initial angular momentum which is mathematically represented as
is the initial angular momentum which is mathematically represented as
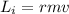
and
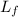 is the final angular momentum which is mathematically represented as
is the final angular momentum which is mathematically represented as
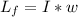
Where I is the moment of inertia of the wheel which is mathematically represented as
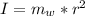
So
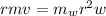
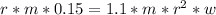
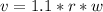
But we know the train is moving relative to the wheel so
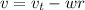
Where wr is the linear velocity component of the wheel so
Substituting values

=>