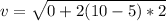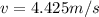Question

A spring gun with a 75 N/m spring constant is loaded with a 5 g foam dart and isaimed vertically. When the spring is compressed by 10 cm and then released, the fireddart rises to a max height of 5 m above the end of the spring gun. Assuming the dartexperiences a constant friction force due to the air, how fast is it traveling when ithas fallen 2 m from its maximum height

Answer 1

The speed is
`v = 4.425 m/s`

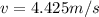
Step-by-step explanation:

From the question we are told that

The spring constant is
`k = 75 \ N /m`

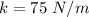
The mass of the foam dart is
`m = 5 g = (5)/(100) = 0.05 \ kg`

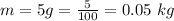
The compression distance is
`d = 10 cm = 0.1 m`

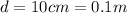
The height which the gun raised the dart is
`h = 5 m`

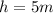
The change in height is
`\Delta h = 2 m`

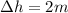
The new height is
`h_2 = 5 -2 = 3 m`

Generally from the law of conservation of energy

`E_s = KE`

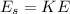
Where
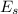`E_s` is the energy stored in spring and it is mathematically represented as

`E_s = (1)/(2) k d^2`

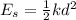
KE is the kinetic energy possessed by the dart when it is being shut and this is mathematically represented as

`KE = (1)/(2) mv^2_r`

So

`(1)/(2) k d^2 = (1)/(2) mv^2_r`

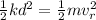
Substituting values

`0.5 * 75 * 0.1 = 0.5 * 0.0005 * v^2_r`

=>
`v_r = \sqrt{(0.5 * 75 * 0.1)/(0.5 * 0.0005 ) }`

`v_r = 12.25 m/s`

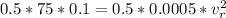
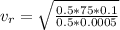
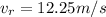
When the dart is at the maximum height the

let it acceleration due air resistance be z

So by equation of motion

`v^2 = u^2 - 2ah`

Where v is the velocity at maximum height which is equal to zero

and u is it initial velocity before reaching maximum height which we calculated as
`v_r = 12.25 m/s`

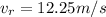
and a is the acceleration due to gravity + the acceleration due to air resistance

So

a = z+g

= 9.8 + z

=>
`v^2 = u^2 - 2(9.8 +z)h`

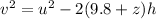
Substituting values

`0 = 12.25^2 - 2(9.8 +z)h`

Making z the subject

`z = ( 12.25)/(2 * 5) - 9.8`

`z = ( 12.25)/(2 * 5) - 9.8`

`z = 5 m/s`

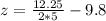
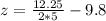
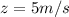
When the dart is moving downward we can mathematically represent the motion as

`v^2 = u^2 + 2ah`

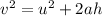
Since the motion is downward and air resistance is upward we have that

a = g - z

and the the initial velocity u becomes the velocity at maximum height

i.e u = 0

And v is the velocity the dart has when it is moving downward

So

`v^2 = 0 + 2 * (g -z )h`

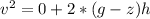
Substituting values

`v = √(0+ 2 (10 - 5) * 2)`

`v = 4.425 m/s`