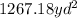Answer:
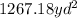
Explanation:
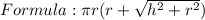
We need;
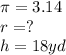
We don't have the radius, but we do have the diameter. A diameter is twice the radius. Therefore, we can divide the diameter by 2 in order to obtain the radius.
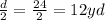
Now plug this info into the formula.
![(3.14)(12yd)[(12yd)+√((18yd)^2+(12yd)^2) ]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/6glnxwz5ximcxkwnyz0wseq0vkybcnxalj.png)
Let's solve the square root first.
![(3.14)(12yd)[(12yd)+√(324yd^2+144yd^2) ]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/6ebqj66ujxc16qptbs0kjjbtmr0ixq6g90.png)
![(3.14)(12yd)[(12yd)+√(468yd^2) ]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/9jqwh7so8ttrvrqsl3ilenmsy5yew070as.png)
![(3.14)(12yd)[(12yd)+√(468yd^2) ]\\(3.14)(12yd)(12yd+21.63yd)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/55cnusxuid0lxoyi3a4w44505uw2tdpqhd.png)
Now solve the sum
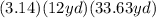
Multiply