Question

g For a specific location in a particularly rainy city, the time a new thunderstorm begins to produce rain (first drop time) is uniformly distributed throughout the day and independent of this first drop time for the surrounding days. Given that it will rain at some point both of the next two days, what is the probability that the first drop of rain will be felt between 9:10 AM and 3:30 PM on at least one of the next two days

Answer 1

The probability that the first drop of rain will be felt between 9:10 AM and 3:30 PM on at least one of the next two days is 0.2639.

Explanation:

The random variable X is defined as the time a new thunderstorm begins to produce rain.

The random variable X is uniformly distributed throughout the day, i.e. between the 24 hours a day or 1440 minutes.

`X\sim Uniform\ [0, 1440]`

The probability density function of X is:

`f_(X)(x)=(1)/(b-a);\ a<X<b,\ a<b`

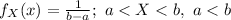
It is provided that it will rain at some point both of the next two days.

Compute the probability that the first drop of rain will be felt between 9:10 AM and 3:30 PM as follows:

9:10 AM = (9 × 60) + 10 = 550 minutes.

3:30 PM = 15:30 = (15 × 60) + 30 = 930 minutes.

Compute the value of P (550 < X < 930) as follows:

`P(550<X<930)=\int\limits^(930)_(550){(1)/(1440-0)}\, dx\\\\=(1)/(1440)* \int\limits^(930)_(550){1}\, dx\\\\=(1)/(1440)* [x]^(930)_(550)\\\\=(930-550)/(1440)\\\\=0.2639`

The probability that the first drop of rain will be felt between 9:10 AM and 3:30 PM is 0.2639.

Then the complement of this event is:

The probability that the first drop of rain will not be felt between 9:10 AM and 3:30 PM is:

P (Not between 9:10 AM and 3:30 PM) = 1 - 0.2639 = 0.7361

Compute the probability that the first drop of rain will be felt between 9:10 AM and 3:30 PM on at least one of the next two days as follows:

P (At least 1) = 1 - P (Less than 1)

= 1 - P (None)

= 1 - P (Not between 9:10 AM and 3:30 PM)

= 1 - 0.7361

= 0.2639

Thus, the probability that the first drop of rain will be felt between 9:10 AM and 3:30 PM on at least one of the next two days is 0.2639.