Question

Let the abbreviation PSLT stand for the percent of the gross family income that goes into paying state and local taxes. Suppose one wants to estimate the mean PSLT for the population of all families in New York City with gross incomes in the range $35.000 to $40.000. If sigma equals 2.0, how many such families should be surveyed if one wants to be 90% sure of being able to estimate the true mean PSLT within .5?

Answer 1

Number of families that should be surveyed if one wants to be 90% sure of being able to estimate the true mean PSLT within 0.5 is at least 43.

Explanation:

We are given that one wants to estimate the mean PSLT for the population of all families in New York City with gross incomes in the range $35.000 to $40.000.

If sigma equals 2.0, we have to find that how many families should be surveyed if one wants to be 90% sure of being able to estimate the true mean PSLT within 0.5.

Here, we will use the concept of Margin of error as the statement "true mean PSLT within 0.5" represents the margin of error we want.

SO, Margin of error formula is given by;

Margin of error =
`Z_(_(\alpha)/(2)_ ) * (\sigma)/(√(n) )`

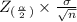
where,
`\alpha` = significance level = 10%

`\sigma` = standard deviation = 2.0

n = number of families

Now, in the z table the critical value of x at 5% (
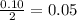`(0.10)/(2) = 0.05` ) level of significance is 1.645.

SO, Margin of error =
`Z_(_(\alpha)/(2)_ ) * (\sigma)/(√(n) )`

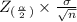
0.5 =
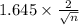
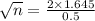
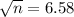
`1.645 * (2)/(√(n) )`

`√(n) =(2* 1.645 )/(0.5)`

`√(n) =6.58`

n =
`6.58^(2)`

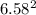
= 43.3 ≈ 43

Therefore, number of families that should be surveyed if one wants to be 90% sure of being able to estimate the true mean PSLT within 0.5 is at least 43.