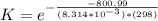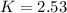Answer:
a
The standard Gibbs free energy change for the reaction at 298 K is
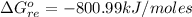
b
The energetic (ΔH) is
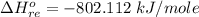
The entropic contributions is
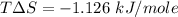
Energetic is the dominant contribution
c
The equilibrium constant at 298 K is
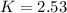
Step-by-step explanation:
From the question we are told that
The chemical reaction is

Generally ,
The free energy of formation of
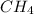 is a constant with a value
is a constant with a value

The free energy of formation of
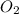 is a constant with a value
is a constant with a value

The free energy of formation of
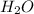 is a constant with a value
is a constant with a value
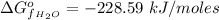
The free energy of formation of
 is a constant with a value
is a constant with a value
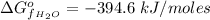
The Enthalpy of formation of
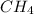 at standard condition i is a constant with a value
at standard condition i is a constant with a value
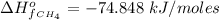
The Enthalpy of formation of
 at standard condition is a constant with a value
at standard condition is a constant with a value
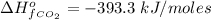
The Enthalpy of formation of
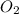 at standard condition is a constant with a value
at standard condition is a constant with a value
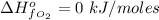
The Enthalpy of formation of
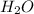 at standard condition is a constant with a value
at standard condition is a constant with a value

The standard Gibbs free energy change for the reaction at 298 K is mathematically represented as
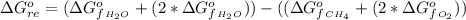
Substituting values
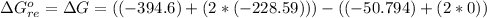
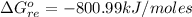
The Enthalpy of formation of the reaction is
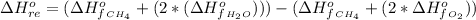
Substituting values
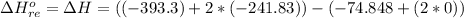
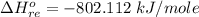
The entropic contributions is mathematically represented as

Substituting values
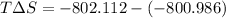
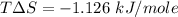
Comparing the values of
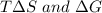 we see that energetic is the dominant contribution
we see that energetic is the dominant contribution
The standard Gibbs free energy change for the reaction at 298 K can also be represented mathematically as
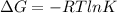
Where R is the gas constant with as value of
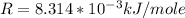
K is the equilibrium constant
T is the temperature with a given value of
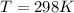
Making K the subject we have
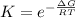
Substituting values