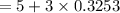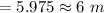Question

An air balloon is moving upward at a constant speed of 3 m/s. Suddenly a passenger realizes that she left her camera on the ground. A friend picks it up and throws it upward at 20 m/s at the instant the passenger is 5 m above the ground. (10 pts) a) Calculate the time for camera to reach passenger. b) Calculate the position and velocity of the camera when passenger catches it.

Answer 1

Answer:t=0.3253 s

Step-by-step explanation:

Given

speed of balloon is
`u=3\ m/s`

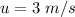
speed of camera
`u_1=20\ m/s`

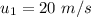
Initial separation between camera and balloon is
`d_o=5\ m`

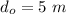
Suppose after t sec of throw camera reach balloon then,

distance travel by balloon is

`s=ut`

`s=3* t`

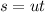
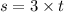
and distance travel by camera to reach balloon is

`s_1=ut+(1)/(2)at^2`

`s_1=20* t-(1)/(2)gt^2`

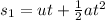
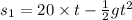
Now

`\Rightarrow s_1=5+s`

`\Rightarrow 20* t-(1)/(2)gt^2 =5+3t`

`\Rightarrow 5t^2-17t+5=0`

`\Rightarrow t=(17\pm √(17^2-4(5)(5)))/(2* 5)`

`\Rightarrow t=(17\pm 13.747)/(10)`

`\Rightarrow t=0.3253\ s\ \text{and}\ t=3.07\ s`

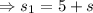
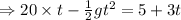
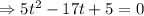
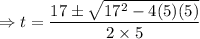
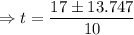
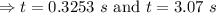
There are two times when camera reaches the same level as balloon and the smaller time is associated with with the first one .

(b)When passenger catches the camera time is
`t=0.3253\ s`

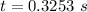
velocity is given by

`v=u+at`

`v=20-10* 0.3253`

`v=16.747\ m/s`

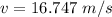
and position of camera is same as of balloon so

Position is
`=5+3* 0.3253`

`=5.975\approx 6\ m`