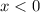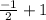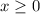Question

Can someone help me out with this one?​

Answer 1


`F(x)=\left \{ {{-(1)/(2)+1, x<0 } \atop {2x-2, x\geq0}} \right.`

Explanation:

There are 2 linear equations, one with an open circle and one with a closed one. Depending on where the circle is, that will tell you your start. Both circles start at 0 on the graph. The open circle means that the first equation will be x < 0. The second equation has a closed circle so it will be
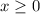`x\geq 0` because the linear equation is increasing positively.

Now you need to the start point of both equations.

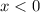`x<0` start point is 1 on the y-axis

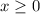`x\geq 0` start point is 2 on the y-axis

Now you have to find the slope for the two equations

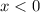`x<0` the equation goes up 1 and and over 2

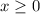`x\geq 0` the equation goes up 2 and over 1

Now put together the equations

`x<0`
`(-1)/(2) + 1`

`x\geq 0`
`2x - 2`