Question

Los Angeles workers have an average commute of 26 minutes. Suppose the LA commute time is normally distributed with a standard deviation of 13 minutes. Let X represent the commute time for a randomly selected LA worker. Round all answers to 4 decimal places where possible.

a. What is the distribution of X? X ~ N(

26

Correct,

13

Correct)


b. Find the probability that a randomly selected LA worker has a commute that is longer than 34 minutes.


c. Find the 70th percentile for the commute time of LA workers.

Answer 1

(a)
`X\sim N(\mu=26,\ \sigma^(2)=13^(2))`.

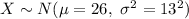(b) The probability that a randomly selected LA worker has a commute that is longer than 34 minutes is 0.2676.

(c) The 70th percentile for the commute time of LA workers is 33 minutes.

Explanation:

The random variable X is defined as the commute time for LA workers.

The mean commute time is, μ = 26 minutes and the standard deviation of the commute times is, σ = 13 minutes.

(a)

It is provided that the LA commute time fr workers is normally distributed.

Then the distribution of the random variable X can be defined as follows:

`X\sim N(\mu=26,\ \sigma^(2)=13^(2))`.

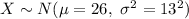(b)

Compute the value of P (X > 34) as follows:

`P(X>34)=P((X-\mu)/(\sigma)>(34-26)/(13))`

`=P(Z>0.62)\\=1-P(Z<0.62)\\=1-0.73237\\=0.26763\\\approx 0.2676`

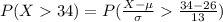
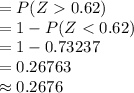
*Use a z-table.

Thus, the probability that a randomly selected LA worker has a commute that is longer than 34 minutes is 0.2676.

(c)

The pth percentile is a data value such that at least p% of the data set is less than or equal to this data value and at least (100 - p)% of the data set are more than or equal to this data value.

The 70th percentile for the commute time of LA workers can be written as follows:

P (X < x) = 0.70

⇒ P (Z < z) = 0.70

The value of z for this probability is:

z = 0.53

*Use a z-table.

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\0.53=(x-26)/(13)\\\\x=26+(0.53* 13)\\\\x=32.89\\\\x\approx 33`

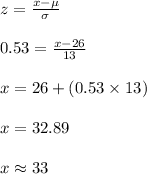
Thus, the 70th percentile for the commute time of LA workers is 33 minutes.