Answer:26.6 miles
Explanation:
Given
Charlie distance to his destination is a linear function of total driving time
suppose distance d is related to time t as
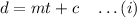
at
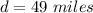 after
after
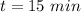
Substitute in (i)
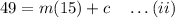
at
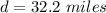 after
after
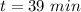
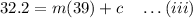
Solving (ii) and (iii) we get
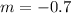
substitute in eq (ii) we get
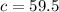
so after
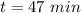
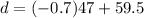
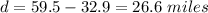
So 26.6 miles is left to travel after 47 minutes