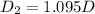Answer:
The diameter of the second pipe is
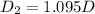
Step-by-step explanation:
From the question we are told that
The length of the connected pipe is
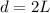
The pressure drop for the first pipe is

The diameter of the pipe is
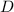
The rate at which the fluid flows for laminar flow is mathematically represented as

Where L is the length of the pipe
 is the dynamic viscosity
is the dynamic viscosity
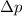 is the difference in pressure
is the difference in pressure
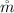 is the flow rate of the fluid
is the flow rate of the fluid
From the equation of continuity
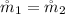
Where
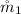 is the flow rate in pipe one
is the flow rate in pipe one
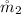 is the flow rate in pipe two
is the flow rate in pipe two
So
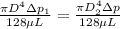
Where
 is the diameter of the second pipe
is the diameter of the second pipe
=>

=>
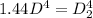
![D_2 =\sqrt[4]{ (D ^4 )/(1.44 ) }](https://img.qammunity.org/2021/formulas/physics/college/asmc81ostg8ipykwxsa2xkdbkmp354qzyq.png)