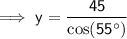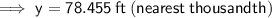Question

Lance, Rachael, and Jamie are playing catch. Lance throws the ball to Rachael, Rachael to Jamie, and Jamie back to Lance. The angle formed at Rachael's position measures 90°. The distance from Lance to Rachael is 45 feet, and the angle formed at Lance's position measures 55°. Lance is trying to determine the other measures created by their positions. Give each measurement rounded to the nearest thousandth of afoot. The angle formed at Jamie's position measures degrees.

Answer 1

35°

64.267 ft

78.455 ft

Explanation:

The given situation can be modeled as a right triangle (see attached).

The interior angles of a triangle sum to 180°

⇒ angle at Jamie's position = 180° - 90° - 55° = 35°

To find the other measures (distances), we can use trig ratios.

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

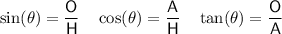
where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle
• H is the hypotenuse

To find the distance from Rachael to Jamie:

`\implies \sf \tan(55^(\circ))=(x)/(45)`

`\implies \sf x=45\tan(55^(\circ))`

`\implies \sf x=64.267\:ft\:(nearest\:thousandth)`

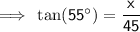
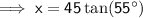
To find the distance from Lance to Jamie:

`\sf \implies \cos(55^(\circ))=(45)/(y)`

`\sf \implies y=(45)/(\cos(55^(\circ)))`

`\sf \implies y=78.455\:ft\:(nearest\:thousandth)`