Question

A sound wave with a frequency of 510 Hz and a wavelength of 3.5 m is directed toward the bottom of a lake to measure its depth. If the echo of the sound from the bottom is heard 0.39 seconds later, how deep is the lake?

Answer 1

Approximately
`2.9 * 10^2 \; \rm m`.

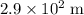Step-by-step explanation:

In that
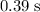`0.39\; \rm s`, this sound wave travelled from the surface of the lake to the bottom, got reflected, and travelled back from the bottom to the surface. The sound wave travelled from the surface to the bottom (without bouncing back) in only
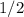`1/2` that much time. In other words, it took only
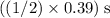`\displaystyle ((1/2) * 0.39)\; \rm s` for the sound wave to travel from the surface to the bottom of the lake.

The speed
`v` of sound in cold water (
`20\; \rm ^\circ C`,
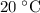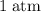`1\; \rm atm`) is approximately
`1.482* 10^(3) \; \rm m \cdot s^(-1)`.

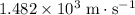In
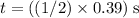`t = ((1/2) * 0.39) \; \rm s`, that sound wave would have travelled a distance of:

`\begin{aligned}s &= v \cdot t \\ &= 1.482 * 10^3 \; \rm m \cdot s^(-1) * \left((1)/(2) * 0.39 \; \rm s\right) \\ &\approx 2.9 * 10^2\; \rm m \end{aligned}`.

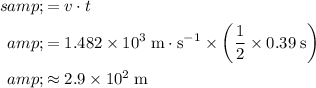Therefore, the depth of the lake is approximately
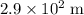`2.9 * 10^2 \; \rm m`.