Question

A 969-kg satellite orbits the Earth at a constant altitude of 99-km. (a) How much energy must be added to the system to move the satellite into a circular orbit with altitude 195 km? 469 Incorrect: Your answer is incorrect. How is the total energy of an object in circular orbit related to the potential energy? MJ (b) What is the change in the system's kinetic energy? MJ (c) What is the change in the system's potential energy?

Answer 1

1.3*10^14 J

Step-by-step explanation:

The energy of the satellite that orbits the earth is given by the second Newton law:

`F=ma_c\\\\-G(mM_s)/(r^2)=m(v^2)/(r)\\\\v^2=(GM)/(r)\\\\E_T=K+U=G(mM_s)/(2r)-G(mM)/(r)=-G(mM)/(2r)`

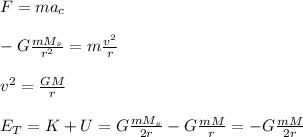
where you have taken into account the centripetal acceleration of the satellite.

m: mass of the satellite

M_s: mass of the sun = 1.98*10^30 kg

G: Cavendish's constant = 6.67*10^-11 m^3/kg s^2

r: distance to the center of the Earth = Earth radius + distance satellite-Earth surface

To find the needed energy, you first compute the energy for a constant altitude of 99km:

r = 6.371*10^6m + 99*10^3m = 6.47*10^6 m

`E_T=-(6.67*10^-11 m^3 /kg.s^2)((969kg)(1.98*10^(30)kg))/(2(6.47*10^6))\\\\E_T=-9.88*10^(15) \ J`

Next, you calculate the energy for an altitude of 195km:

r = 6.371*10^6m + 195*10^{3}m = 6.56*10^6 m

`E_T=-(6.67*10^-11 m^3 /kg.s^2)((969kg)(1.98*10^(30)kg))/(2(6.56*10^6))\\\\E_T=-9.75*10^(15) \ J`

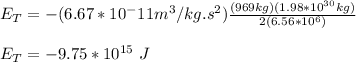
Finally, the energy required to put the satellite in the new orbit is:

-9.75*10^15 J - (-9.88*10^15 J) = 1.3*10^14 J