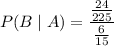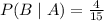Answer:(a)
Explanation:
Given
There are 4 yellow, 6 green and 5 blue marbles
We have to find
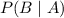 i.e. conditional probability of B given that A is occurred.
i.e. conditional probability of B given that A is occurred.
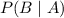 is given by
is given by

Also A=drawing a green marble
B=drawing a yellow marble
Total no of marbles
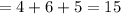
So,

similarly
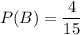
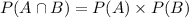
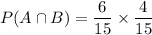

Substituting the values in the formula