Question

Find the two geometric means between 20 and 2500

Answer 1

The two geometric means between 20 and 2500 are 100 and 500.

Explanation:

First of all we all should know about a geometric progression to solve this question.

A geometric progression is a series in which there is a first term a and all the next terms are calculated by multiplying the previous term by a common number r.

where a is known as first term and

r is known as common ratio.

In the question we are given a as 20 and we have to find out 2 terms after 20 and 4th term is given as 2500.

Formula for
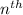`n^(th)` term in a geometric progression is:

`a_(n) = a* r^(n-1)`

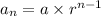
Here
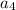`a_(4)` = 2500

As per formula of
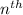`n^(th)` term:

`a* r^(3) = 2500\\\Rightarrow 20 * r^(3) =2500\\\Rightarrow r^(3) = 125\\\Rightarrow r = 5`

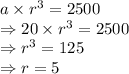
Now, 2nd term:

`a_(2) = a * r\\\Rightarrow a_(2) = 20 * 5\\\Rightarrow a_(2) = 100`

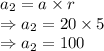
Now, 3rd term:

`a_(3) = a * r^(2) \\\Rightarrow a_(3) = 20 * 5^(2)\\\Rightarrow a_(3) = 500`

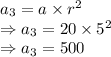
So, the two geometric means between 20 and 2500 are 100 and 500.