Answer:
a) 2.4 mm
b) 1.2 mm
c) 1.2 mm
Step-by-step explanation:
To find the widths of the maxima you use the diffraction condition for destructive interference, given by the following formula:
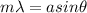
a: width of the slit
λ: wavelength
m: order of the minimum
for little angles you have:
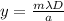
y: height of the mth minimum
a) the width of the central maximum is 2*y for m=1:
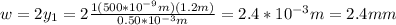
b) the width of first maximum is y2-y1:
![w=y_2-y_1=((500*10^(-9)m)(1.2m))/(0.50*10^(-3)m)[2-1]=1.2mm](https://img.qammunity.org/2021/formulas/physics/college/98c89ds5cywdomchowztmpcg4ljw6g8p02.png)
c) and for the second maximum:
![w=y_3-y_2=((500*10^(-9)m)(1.2m))/(0.50*10^(-3)m)[3-2]=1.2mm](https://img.qammunity.org/2021/formulas/physics/college/jw7cpfwu0cq2bs7lh3tszzs1ap79dork7w.png)