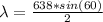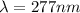Question

A single slit forms a diffraction pattern, with the first minimum at an angle of 40 degrees from central maximum. Monochromatic light of 410 nm wavelength is used. The same slit, illuminated by a different monochromatic light source, produces a diffraction pattern with the second minimum at a 60 degree angle from the central maximum. The wavelength of this light, in nm, is closest to:

Answer 1

The wavelength of the second monochromatic light is
`\lambda = 277 nm`

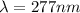
Step-by-step explanation:

From the question we are told that

The angle of the first minimum is
`\theta_1 = 40^o`

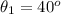
The wavelength of the first monochromatic light is
`\lambda_1 = 410 \ nm`

The angle of the second minima is
`\theta_2 = 60^o`

For the first minima the distance of separation of diffraction patterns is mathematically represented as

`a = (\lambda_1 )/(sin \theta_1)`

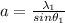
Substituting values

`a = (410 *10^(-9))/(sin (40) )`

`a = 638 nm`

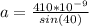
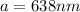
The distance between two successive diffraction is constant for the same slit

Thus the wavelength of the second light is

`\lambda = (a * sin (60))/(2)`

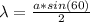
Substituting value

`\lambda = (638 * sin (60))/(2)`

`\lambda = 277 nm`

Answer 2

276.19nm

Step-by-step explanation:

To find the other wavelength you use the following condition for the diffraction of both wavelengths:

`m_1\lambda_1=asin\theta_1\\\\m_2\lambda_2=asin\theta_2\\\\` ( 1 )

λ1=410nm

m=1 for wavelength 1

m=2 for wavelength 2

a: width of the slit

θ1: angle of the first minimum

θ2: angle of the second minimum

you divide both equations and you obtain:

`(m_1\lambda_1)/(m_2\lambda_2)=(sin\theta_1)/(sin\theta_2)\\\\\lambda_2=(sin\theta_2)/(sin\theta_1)(m_1\lambda_1)/(m_2)\\\\\lambda_2=(sin60\°)/(sin40\°) ((1)(410nm))/(2)=276.19nm`

hence, the wavelength of the second monochromatic wave is 276.19nm