Question

In ΔIJK, the measure of ∠K=90°, KJ = 77, IK = 36, and JI = 85. What ratio represents the cosine of ∠I?

Answer 1

the ratio of cosine of angle I is 36/85.

Explanation:

Answer 2

We have been given that in ΔIJK, the measure of ∠K=90°, KJ = 77, IK = 36, and JI = 85. We are asked to find the ratio that represents the cosine of angle I.

First of all, we will draw a right triangle as shown in the attachment.

We know that cosine relates adjacent side of right triangle with hypotenuse.

`\text{cos}=\frac{\text{Adjacent}}{\text{Hypotenuse}}`

We can see that adjacent side to angle I is IK and hypotenuse is IJ.

`\text{cos}(\angle I)=(IK)/(IJ)`

`\text{cos}(\angle I)=(36)/(85)`

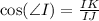
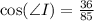
Therefore, the ratio of cosine of angle I is
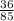`(36)/(85)`.