Answer:
There is not enough evidence to reject the null hypothesis.
Explanation:
(a)
The hypothesis can be defined as follows:
H₀: p₁ - p₂ ≤ 0 vs. Hₐ: p₁ - p₂ > 0.
(b)
The test statistic is defined as follows:
![z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{\hat P(1-\hat P)[(1)/(n_(1))+(1)/(n_(2))]}}](https://img.qammunity.org/2021/formulas/mathematics/college/szor0t2rj23ygfyhvxf7xokxb8oasg227n.png)
The information provided is:
n₁ = 244
n₂ = 311
x₁ = 122
x₂ = 137
Compute the sample proportions and total proportions as follows:
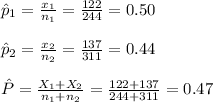
Compute the test statistic value as follows:
![z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{\hat P(1-\hat P)[(1)/(n_(1))+(1)/(n_(2))]}}](https://img.qammunity.org/2021/formulas/mathematics/college/szor0t2rj23ygfyhvxf7xokxb8oasg227n.png)
![=\frac{0.50-0.44}{\sqrt{0.47(1-0.47)[(1)/(244)+(1)/(311)]}}\\\\=1.41](https://img.qammunity.org/2021/formulas/mathematics/college/r7jl1kydt1my6qd4dc4hg87kp9r0rl49as.png)
The test statistic value is 1.41.
The decision rule is:
The null hypothesis will be rejected if the p-value of the test is less than the significance level α = 0.05.
Compute the p-value as follows:
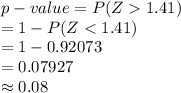
*Use a z-table.
The p-value of the test is 0.08.
p-value = 0.08 > α = 0.05
The null hypothesis will not be rejected at 5% significance level.
Thus, there is not enough evidence to reject the null hypothesis.