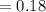Answer:
Allele frequency
Normal allele
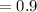
Mutant r allele

Genotype frequency
Homozygous normal bugs
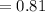
Homozygous mutant bug
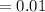
Heterozygous normal bug with one mutant r allele and one normal allele
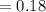
Step-by-step explanation:
It is given that 99% of the bugs were killed after the spray of pyrethrum. This suggests that 1% of the bugs that were not killed must be homozygous for the mutant type allele "r"
Thus, the frequency of homozygous "rr" species i.e
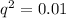
From this we can evaluate the frequency of mutant "r" allele.
Thus,
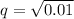
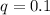
As per Hardy-Weinberg first equilibrium equation,
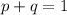
Substituting the value of q in above equation, we get
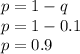
Thus, the frequency of homozygous normal bug is equal to
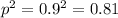
As per Hardy-Weinberg second equilibrium equation-
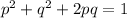
Substituting all the available values we get -

Allele frequency
Normal allele
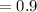
Mutant r allele

Genotype frequency
Homozygous normal bugs
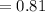
Homozygous mutant bug
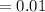
Heterozygous normal bug with one mutant r allele and one normal allele