Question

A recent survey by the New Statesman on British social attitudes asked respondents if they believe that inequality is too large. The survey found that 74% of the respondents do believe inequality is too large. In a sample of six British citizens, what is the probability that two believe inequality is too large? In a sample of six British citizens, what is the probability that at least two respondents believe that inequality is too large? In a sample of four British citizens, what is the probability that none believe inequality is too large?

Answer 1

(a) The probability that in a a sample of six British citizens two believe inequality is too large is 0.0375.

(b) The probability that in a a sample of six British citizens at least two believe inequality is too large is 0.9944.

(c) The probability that in a a sample of four British citizens none believe inequality is too large is 0.0046.

Explanation:

The random variable X can be defined as the number of British citizens who believe that inequality is too large.

The proportion of respondents who believe that inequality is too large is, p = 0.74.

Thus, the random variable X follows a Binomial distribution with parameters n and p = 0.74.

The probability mass function of X is:

`P(X=x)={n\choose x}\ 0.74^(x)(1-0.74)^(n-x);\ x=0,1,2,3...n`

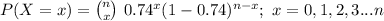
(a)

Compute the probability that in a a sample of six British citizens two believe inequality is too large as follows:

`P(X=2)={6\choose 2}\ 0.74^(2)(1-0.74)^(6-2)\\=15* 0.5476* 0.00456976\\=0.03753600864\\\approx 0.0375`

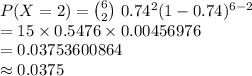
Thus, the probability that in a a sample of six British citizens two believe inequality is too large is 0.0375.

(b)

Compute the probability that in a a sample of six British citizens at least two believe inequality is too large as follows:

P (X ≥ 2) = 1 - P (X < 2)

= 1 - P (X = 0) - P (X = 1)

`=1-[{6\choose 0}\ 0.74^(0)(1-0.74)^(6-0)]-[{6\choose 1}\ 0.74^(1)(1-0.74)^(6-1)]\\\\=1-[1* 1* 0.000308915776]-[6* 0.74* 0.0011881376]\\\\=1-0.00031-0.0053\\\\=0.99439\\\\\approx 0.9944`

Thus, the probability that in a a sample of six British citizens at least two believe inequality is too large is 0.9944.

(c)

Compute the probability that in a a sample of four British citizens none believe inequality is too large as follows:

`P(X=0)={4\choose 0}\ 0.74^(0)(1-0.74)^(4-0)\\=1* 1* 0.00456976\\=0.00456976\\\approx 0.0046`

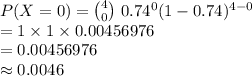
Thus, the probability that in a a sample of four British citizens none believe inequality is too large is 0.0046.