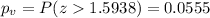Question

a nationwide study of american homeowners revealed that​ 65% own at least one lawn mower. a lawn equipment​ manufacturer, located in​ charlotte, feels that this estimate is too low for households in charlotte. to support his​ claim, he randomly selects 497 homes in charlotte and finds that 340 had one or more lawn mowers. find the​ p-value for testing the claim that the proportion of homeowners owning lawn mowers in charlotte is higher than​ 65%. round your answer to three decimal places. when you calculate the sample proportion keep 4 decimal places.

Answer 1

`z=\frac{0.6841 -0.65}{\sqrt{(0.65(1-0.65))/(497)}}=1.5938`

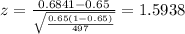
We have a right tailed test then the p value would be:

`p_v =P(z>1.5938)=0.0555`

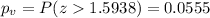
Explanation:

Information provided

n=497 represent the random sample of homes selected

X=340 represent the number of homes with one or more lawn

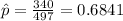`\hat p=(340)/(497)=0.6841` estimated proportion of homes with one or more lawn

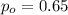`p_o=0.65` is the value that we want to test

z would represent the statistic

`p_v` represent the p value (variable of interest)

System of hypothesis

We want to check if proportion of homeowners owning lawn mowers in charlotte is higher than​ 65%m so then the correct hypothesis are .:

Null hypothesis:
`p\leq 0.65`

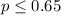
Alternative hypothesis:
`p > 0.65`

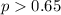
The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.6841 -0.65}{\sqrt{(0.65(1-0.65))/(497)}}=1.5938`

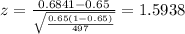
We have a right tailed test then the p value would be:

`p_v =P(z>1.5938)=0.0555`