Answer:
The slopes are different, and the y-intercepts are different.
Explanation:
When we have an equation with the form: y=mx+b
m is the slope and b is the intercept.
So, for the first equation: 4x + 2y = -2, we can solve for y as:
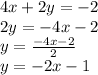
Then, the slope of this equation is -2 and the intercept is -1
At the same way, for the second equation: x-3y=24, we can solve for y as:
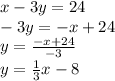
Then the slope of this equation is
 and the intercept is -8
and the intercept is -8
Finally, we can conclude that the slopes are different, and the y-intercepts are different.