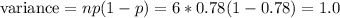Question

​78% of U.S. adults think that political correctness is a problem in America today. You randomly select six U.S. adults and ask them whether they think that political correctness is a problem in America today. The random variable represents the number of U.S. adults who think that political correctness is a problem in America today. Answer the questions below.

Find the mean of the binomial distribution ​(Round to the nearest tenth as​ needed.)Find the variance of the binomial distribution. (Round to the nearest tenth as​ needed.)

Answer 1

mean = 4.9

variance = 1.0

Explanation:

An American thinks that political correctness is a problem or does not think that it is a problem therefore the distribution of the random variable is binomial and for this case the parameters of it would be

`n = 6 \\p = 0.78\\`

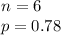
Then the formula for the mean is

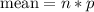`\text{mean} = n*p`, which is 6*0.78 = 4.9,

The formula for variance is

`\text{variance} = np(1-p) = 6*0.78(1-0.78) = 1.0`

Answer 2

mean= 4.68

variance= 1.0296

Explanation:

mean= n×p

n=6

p=0.78

mean= 6×(0.78)

= 4.68

variance= n×p×(1-p)

= 6 × 0.78×(1-0.78)

= 1.0296