Question

You are the manager of a restaurant for a​ fast-food franchise. Last​ month, the mean waiting time at the​ drive-through window for branches in your geographical​ region, as measured from the time a customer places an order until the time the customer receives the​ order, was 3.9 minutes. You select a random sample of 64 orders. The sample mean waiting time is 4.03 ​minutes, with a sample standard deviation of 0.8 minutes. Complete parts​ (a) and​ (b) below.

a. Determine the test statistic.(two decimal places)
b. Find the​ p-value.(three decimal places)
c. What is the conclusion?

Answer 1

(a) The test statistics is 1.30.

(b) The P-value is 0.198.

(c) We conclude that the mean waiting time was equal to 3.9 minutes.

Explanation:

We are given that the mean waiting time at the​ drive-through window for branches in your geographical​ region, as measured from the time a customer places an order until the time the customer receives the​ order, was 3.9 minutes.

You select a random sample of 64 orders. The sample mean waiting time is 4.03 ​minutes, with a sample standard deviation of 0.8 minutes.

Let
`\mu` = mean waiting time at the​ drive-through window for branches in your geographical​ region.

So, Null Hypothesis,
`H_0` :
`\mu` = 3.9 minutes {means that the mean waiting time was equal to 3.9 minutes}

Alternate Hypothesis,
`H_A` :
`\mu\\eq` 3.9 minutes {means that the mean waiting time was different from 3.9 minutes}

The test statistics that would be used here One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean waiting time = 4.03 minutes

s = sample standard deviation = 0.8 minutes

n = sample of orders = 64

So, test statistics =
`(4.03-3.9)/((0.8)/(√(64) ) )` ~
`t_6_3`

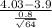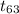
= 1.30

(a) The value of t test statistics is 1.30.

(b) The P-value of the test statistics is given by;

P-value = P(
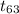`t_6_3` > 1.30) = 0.099

For two tailed test, p-value is calculated as = 0.099
`*` 2 = 0.198

(c) Since, in the question we are not given with the level of significance so we assume it to be 5%.

Now, P-value of the test statistics is more than the level of significance as 0.198 > 0.05, so we have insufficient evidence to reject our null hypothesis.

Therefore, we conclude that the mean waiting time was equal to 3.9 minutes.