Question

A bank with a branch located in a commercial district of a city has the business objective of developing an improved process for serving customers during the noon-to-1 p.m. lunch period. Management decides to first study the waiting time in the current process. The waiting time is defined as the number of minutes that elapses from when the customer enters the line until he or she reaches the teller window. Data are collected from a random sample of 15 customers and stored in Bank1 .

These data are:

4.21 5.55 3.02 5.13 4.77 2.34 3.54 3.20 4.50 6.10 0.38 5.12 6.46 6.19 3.79

Required:
a. Determine the test statistic.
b. Determine the critical? value(s).

Answer 1

(a) The test statistic value is -4.123.

(b) The critical values of t are ± 2.052.

Explanation:

In this case we need to determine whether there is evidence of a difference in the mean waiting time between the two branches.

The hypothesis can be defined as follows:

H₀: There is no difference in the mean waiting time between the two branches, i.e. μ₁ - μ₂ = 0.

Hₐ: There is a difference in the mean waiting time between the two branches, i.e. μ₁ - μ₂ ≠ 0.

The data collected for 15 randomly selected customers, from bank 1 is:

S = {4.21, 5.55, 3.02, 5.13, 4.77, 2.34, 3.54, 3.20, 4.50, 6.10, 0.38, 5.12, 6.46, 6.19, 3.79}

Compute the sample mean and sample standard deviation for Bank 1 as follows:

`\bar x_(1)=(1)/(n_(1))\sum X_(1)=(1)/(15)[4.21+5.55+...+3.79]=4.29`

`s_(1)=\sqrt{(1)/(n_(1)-1)\sum (X_(1)-\bar x_(1))^(2)}\\=\sqrt{(1)/(15-1)[(4.21-4.29)^(2)+(5.55-4.29)^(2)+...+(3.79-4.29)^(2)]}\\=1.64`

The data collected for 15 randomly selected customers, from bank 2 is:

S = {9.66 , 5.90 , 8.02 , 5.79 , 8.73 , 3.82 , 8.01 , 8.35 , 10.49 , 6.68 , 5.64 , 4.08 , 6.17 , 9.91 , 5.47}

Compute the sample mean and sample standard deviation for Bank 2 as follows:

`\bar x_(2)=(1)/(n_(2))\sum X_(2)=(1)/(15)[9.66+5.90+...+5.47]=7.11`

`s_(2)=\sqrt{(1)/(n_(2)-1)\sum (X_(2)-\bar x_(2))^(2)}\\=\sqrt{(1)/(15-1)[(9.66-7.11)^(2)+(5.90-7.11)^(2)+...+(5.47-7.11)^(2)]}\\=2.08`

(a)

It is provided that the population variances are not equal. And since the value of population variances are not provided we will use a t-test for two means.

Compute the test statistic value as follows:

`t=\frac{\bar x_(1)-\bar x_(2)}{\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))}}`

`=\frac{4.29-7.11}{\sqrt{(1.64^(2))/(15)+(2.08^(2))/(15)}}`

`=-4.123`

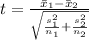
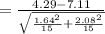
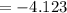
Thus, the test statistic value is -4.123.

(b)

The degrees of freedom of the test is:

`m=([(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))]^(2))/((((s_(1)^(2))/(n_(1)))^(2))/(n_(1)-1)+(((s_(2)^(2))/(n_(2)))^(2))/(n_(2)-1))`

`=([(1.64^(2))/(15)+(2.08^(2))/(15)]^(2))/((((1.64^(2))/(15))^(2))/(15-1)+(((2.08^(2))/(15))^(2))/(15-1))`

`=26.55\\\approx 27`

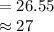
Compute the critical value for α = 0.05 as follows:

`t_(\alpha/2, m)=t_(0.025, 27)=\pm2.052`

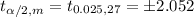
*Use a t-table for the values.

Thus, the critical values of t are ± 2.052.