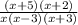Answer:
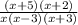
Explanation:
The given expression is
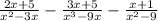
First, we need to factor each denominator
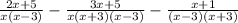
So, the least common factor (LCF) is
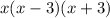 , because they are the factors that repeats.
, because they are the factors that repeats.
Now, we diviide the LCF by each denominator, to then multiply it by each numerator.
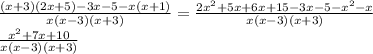
Then, we factor the numerator, to do so, we need to find two numbers which product is 10 and which sum is 7.
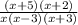
Therefore, the expression is equivalent to