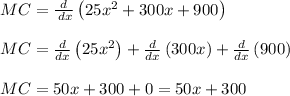Question

A bakery finds that the price they can sell cakes is given by the function p = 580 − 10x where x is the number of cakes sold per day, and p is price. The total cost function of the company is given by c = (30+5x) 2 where x is previously defined, and c is total cost.

Find the revenue and marginal revenue functions [Hint: revenue is price multiplied by quantity i.e. revenue = price × quantity] (3 marks)

Working and Answer Space for Part A









Find the fixed cost and marginal cost function [Hint: fixed cost does not change with quantity produced] (3 marks)

Working and Answer Space for Part

Answer 1

The total revenue is
`TR=580x-10x^2`.

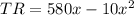The marginal revenue is
`MR=580-20x`.

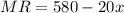The fixed cost is $900.

The marginal cost function is
`MC=50x+300`.

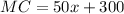Explanation:

The Total Revenue (
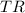`TR`) received from the sale of
`x` goods at price
`p` is given by

`TR=p\cdot x`

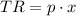
The Marginal Revenue (
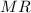`MR`) is the derivative of total revenue with respect to demand and is given by

`MR=(d(TR))/(dx)`

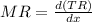
From the information given we know that the price they can sell cakes is given by the function
`p=580-10x`, where
`x` is the number of cakes sold per day.

So, the total revenue is

`TR=(580-10x)\cdot x\\TR=580x-10x^2`

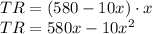
And the marginal revenue is

`MR=(d)/(dx)(580x-10x^2) \\\\\mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g'\\\\MR=(d)/(dx)\left(580x\right)-(d)/(dx)\left(10x^2\right)\\\\MR=580-20x`

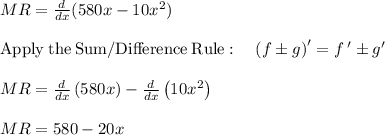
The Fixed Cost (
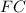`FC`) is the amount of money you have to spend regardless of how many items you produce.

The Marginal Cost (
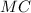`MC`) function is the derivative of the cost function and is given by

`MC=(d(TC))/(dx)`

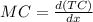
We know that the total cost function of the company is given by
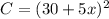`C=(30+5x)^2`, which it is equal to

`\mathrm{Apply\:Perfect\:Square\:Formula}:\quad \left(a+b\right)^2=a^2+2ab+b^2\\a=30,\:\:b=5x\\\\\left(30+5x\right)^2=30^2+2\cdot \:30\cdot \:5x+\left(5x\right)^2=25x^2+300x+900\\\\C=25x^2+300x+900`

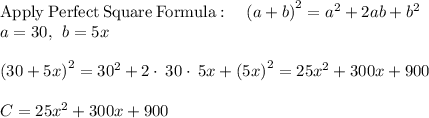
From the total cost function and applying the definition of fixed cost, the fixed cost is $900.

And the marginal cost function is

`MC=(d)/(\:dx)\left(25x^2+300x+900\right)\\\\MC=(d)/(dx)\left(25x^2\right)+(d)/(dx)\left(300x\right)+(d)/(dx)\left(900\right)\\\\MC=50x+300+0=50x+300`