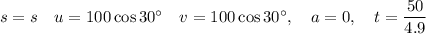Question

The projectile is fired with initial velocity of 100ms-1 at an angle of 30° with the horinzontal.Calculate a.The time of flight b.The maximum height attained c.The range​

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Here,

• The projectile is fired with initial velocity =100m/s
• The Angle formed with the horizontal = 30°

Answer (a)

Here, we have

• Initial velocity = 100 m/s
• Angle of projection = 30°

We have to find the time of flight

We know that,

Time of flight

`\sf{ = }{\sf{\frac{ 2uSin{\theta}}{g}}}`

Subsitute the required values,

`\sf{ = }{\sf{\frac{ 2{*}100{*}Sin30{\degree}}{9.8}}}`

`\sf{ = }{\sf{\frac{ 200{*}{(1)/(2)}}{9.8}}}`

`\sf{ = }{\sf{( 100)/(9.8)}}`

`\bold{ = 10.20 \: s }`

Hence, The time of flight is 10.20 sec .

Answer (b)

Here, We have

• Initial velocity = 100 m/s
• Angle of projection = 30°

We have to find the maximum height attained by the body

We know that,

Maximum height

`\sf{ = }{\sf{\frac{ u^(2)Sin^(2){\theta}}{2g}}}`

Subsitute the required values,

`\sf{ = }{\sf{\frac{ (100)^(2){*}Sin^(2)30{\degree}}{2{*} 9.8}}}`

`\sf{ = }{\sf{\frac{ 10000{*}{(1)/(2)}{*}{(1)/(2)}}{19.6}}}`

`\sf{ = }{\sf{\frac{ 5000{*}{(1)/(2)}}{19.6}}}`

`\sf{ = }{\sf{( 2500)/(19.6)}}`

`\sf{ = 127.5 \: m}`

Hence, The maximum height attained by the body is 127.5 .

Answer ( c) :-

Here, we have

• Initial velocity = 100 m/s
• Angle of projection = 30°

We have to find the horizontal range

We know that,

Horizontal range

`\sf{ = }{\sf{\frac{ u^(2)Sin2{\theta}}{g}}}`

Subsitute the required values,

`\sf{ = }{\sf{\frac{ (100)^(2){*}Sin2{*}30{\degree}}{9.8}}}`

`\sf{ = }{\sf{\frac{ 10000{*}Sin{*}60{\degree}}{9.8}}}`

`\sf{ = }{\sf{\frac{ 10000{*}{(√(3))/(2)}}{9.8}}}`

`\sf{ = }{\sf{\frac{ 5000{*}√(3)}{9.8}}}`

`\sf{ = }{\sf{\frac{ 5000{*}1.732}{9.8}}}`

`\sf{ = }{\sf{( 8660)/(9.8)}}`

`\sf{ = 883.67 \: or 883.7 m}`

Hence, The range of the body is 883.67 or 883.7 m.

Answer 2

(a) 10.20 s (nearest hundredth)

(b) 127.55 m (nearest hundredth)

(c) 883.70 m (nearest hundredth)

Step-by-step explanation:

Part (a)

At the end of the projectile's flight, its vertical displacement will be zero.

Resolving vertically, taking up as positive:

`s=0\quad u=100 \sin30^(\circ) \quad v=v, \quad a=-9.8, \quad t=t`

`\begin{aligned}\textsf{Using }\:s & =ut+\frac12at^2:\\ 0 & =100 \sin 30^(\circ)t+\frac12(-9.8)t^2\\ 0 & = 50t-4.9t^2\\ 4.9t^2 & = 50t\\ 4.9t & = 50\\ t & = (50)/(4.9)\\ t & = 10.20\:\sf s\:(nearest\:hundredth)\end{aligned}`

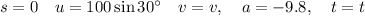
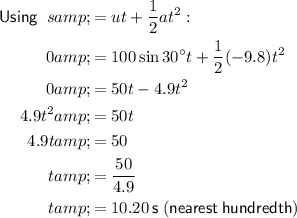
Part (b)

At the maximum height, vertical velocity will be zero.

Resolving vertically, taking up as positive:

`s=0\quad u=100 \sin30^(\circ) \quad v=0, \quad a=-9.8, \quad t=t`

`\begin{aligned}\textsf{Using }\:v^2 & = u^2+2as :\\ 0^2 & = (100 \sin 30^(\circ))^2+2(-9.8)s\\ 0 & = 2500-19.6s\\ 19.6s & = 2500\\ s & = (2500)/(19.6)\\ s & = 127.55\: \sf m\:(nearest\:hundredth) \end{aligned}`

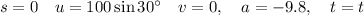
Part (c)

The horizontal velocity of a projectile is always constant, so u = v.

The horizontal component of acceleration is zero.

Resolving horizontally, taking right as positive (and using the value for t we found in part a):

`s=s\quad u=100 \cos30^(\circ) \quad v=100 \cos30^(\circ) , \quad a=0, \quad t=(50)/(4.9)`

`\begin{aligned}\textsf{Using }\:s & =ut+\frac12at^2 : \\ s & =(100 \cos 30^(\circ))\left((50)/(4.9)\right)+\frac12(0)\left((50)/(4.9)\right)^2\\ s & =50√(3)\left((50)/(4.9)\right)+0\\ s & =883.70\: \sf m\:(nearest\:hundredth)\end{aligned}`