Question

A simple random sample with provided a sample mean of and a sample standard deviation of . a. Develop a confidence interval for the population mean (to 1 decimal). , b. Develop a confidence interval for the population mean (to 1 decimal). , c. Develop a confidence interval for the population mean (to 1 decimal). , d. What happens to the margin of error and the confidence interval as the confidence level is increased?

Answer 1

Question:

A simple random sample with n=54 provided a sample mean of 22.5 and a sample standard deviation of 4.4.

a. Develop a 90% confidence interval for the population mean.

b. Develop a 95% confidence interval for the population mean.

c. Develop a 99% confidence interval for the population mean.

d. What happens to the margin of error and the confidence interval as the confidence level is increased?

Answer:

a. CI = 21.4976 ≤ μ ≤ 23.5024

b. CI = 21.29903 ≤ μ ≤ 23.70097

c. CI = 20.90021 ≤ μ ≤ 24.09979

d. The margin of error and confidence interval increases

Explanation:

Here we have

Sample size, n = 54

Mean,
`\bar{x}` = 22.5

s = 4.4

a. The confidence interval, CI is;

`CI=\bar{x}\pm t_(\alpha/2) * (s)/(√(n))`

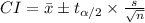
At c = 90% confidence level,
`t_(\alpha/2)` with degrees of freedom, df = n - 1 = 54 - 1 = 53 and α = (1 - c)/2 = (1 - 0.9)/2 = 0.05, from the t table or relation we will find

`t_(\alpha/2)` = 1.674116

Therefore, plugging in the values, we have

CI at 90% gives

`CI=22.5\pm 1.674 * (4.4)/(√(54))`

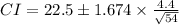
or CI = 21.4976 ≤ μ ≤ 23.5024

b. For c = 95%, α = (1 - 0.95)/2 = 0.025, df = 54 - 1 = 53

From tables or t relations,
`t_(\alpha/2)` = 2.005746

∴
`CI=22.5\pm 2.005746 * (4.4)/(√(54))`

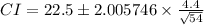
or CI = 21.29903 ≤ μ ≤ 23.70097

c. For c = 99%, α = (1 - 0.99)/2 = 0.005, df = 54 - 1 = 53

From tables or t relations,
`t_(\alpha/2)` = 2.671822

∴
`CI=22.5\pm 2.671822* (4.4)/(√(54))`

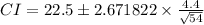
or CI = 20.90021 ≤ μ ≤ 24.09979

d. As the confidence level is increased,
`t_(\alpha/2)` increases, therefore, the margin of error and confidence interval increases.