Question

We intend to estimate the average break time of Dunder Mifflin employees. From a previous study, we believe that the average time is 42 minutes with a standard deviation of 6 minutes. We want our 99 percent confidence interval to have a margin of error of no more than plus or minus 2 minutes. What is the smallest sample size that we should consider?

Answer 1

`n=((2.58(6))/(2))^2 =59.907 \approx 60`

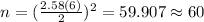
So we need a sample of at least 60 in order to satisfy the condition.

Explanation:

Notation

`\bar X` represent the sample mean

`\mu` population mean (variable of interest)

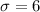`\sigma=6` represent the population standard deviation assumed

n represent the sample size

Solution

The confidence interval for the mean is given by the following formula:

`\bar X \pm z_(\alpha/2)(\sigma)/(√(n))` (1)

The margin of error is given by this formula:

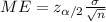`ME=z_(\alpha/2)(\sigma)/(√(n))` (2)

And on this case we have that ME =2 and we are interested in order to find the value of n, if we solve n from equation (2) we got:

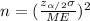`n=((z_(\alpha/2) \sigma)/(ME))^2` (3)

The critical value for 99% of confidence interval now can be founded using the normal distribution. And in excel we can use this formula to find it:"=-NORM.INV(0.005;0;1)", and we got
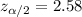`z_(\alpha/2)=2.58`, replacing into formula (3) we got:

`n=((2.58(6))/(2))^2 =59.907 \approx 60`

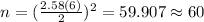
So we need a sample of at least 60 in order to satisfy the condition.

Answer 2

The minimum sample size that we should consider is of 60 employees.

Explanation:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.99)/(2) = 0.005`

Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`.

So it is z with a pvalue of
`1-0.005 = 0.995`, so
`z = 2.575`

Now, find the margin of error M as such

`M = z*(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

We want our 99 percent confidence interval to have a margin of error of no more than plus or minus 2 minutes. What is the smallest sample size that we should consider?

We need to find n for which
`M = 2, \sigma = 6`

So

`M = z*(\sigma)/(√(n))`

`2 = 2.575*(6)/(√(n))`

`2√(n) = 2.575*6`

Simplifying by 2

`√(n) = 2.575*3`

`(√(n))^(2) = (2.575*3)^(2)`

`n = 59.67`

Rounding up

The minimum sample size that we should consider is of 60 employees.